K - Nearest Neighbors Algorithm (K-NN)

Introduction

Another categorical method of prediction. KNN takes a comparison approach, where new data point is compared to other points that are close by.

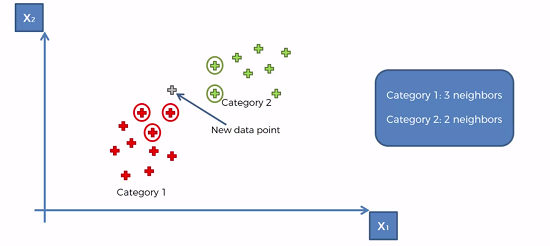
It works as shown in the graph below. The Euchlidian distance is calculated between the 5 closest data points. And simply just assign the new data point to the category with largest number of nearest neighbors, in this case it would be category 1.

Steps for KNN

1. Choose the number k of neighbors (default is usually 5)
2. Take the K nearest neighbors of the new data point, accoding to the Euclidean distance (or any other distance formula)
3. Among these K neighbors, count the number of data points in each category
4. Assign the new data point to the category where you counted the most neighbors

Building the K-NN in Python

Use classsification Template and preprocess the data.

import kNeighborsClassifier from the sklearn.neighbors library and fit the object to the training set.

‘KNeighborsClassifier’ has the following parameters : n_neighbors : # of neighbors to use metric : Distance metric for use for tree. Use ‘minkowski’ p : Power parameter. Euclidean distance = 2.

from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifiers(n_neighbors = 5, metric = 'minkowski', p = 2)
classifier.fit(X_train, y_train)